I’ve been long fascinated by the endless online debates about whether the infinite decimal expansion 0.9999… is exactly equal to 1. The canonical answer is yes. But there’s a considerable number of blogs that will try to convince you otherwise — and in the process, expose the sinister machinations of Big Math.
What’s unique about this situation is that while it feels like bog-standard online crackpottery, it’s sort of running in reverse. The belief that 0.x must be less than 1.y makes perfect sense to rational people. Any website that tries to convince you otherwise probably also has some posts about chemtrails and reptilian mind control?…
The end result is that despite the existence of various proofs, the educators pretty consistently fail to impress this concept upon students. It’s interesting to ponder why. Consider the most common elementary sorta-proof:
\(\begin{array}{c} \frac{1}{3} = 0.3333\ldots \\ \\ \underbrace{3 \cdot \frac{1}{3}}_{= \ 1} = 3 \cdot 0.3333 \ldots = 0.9999\ldots \\ \end{array}\)
Hmm… are we representing the infinite decimal expansion of 1 ÷ 3 correctly? What does it even mean to write “…”? Is it OK to multiply an infinite decimal expansion by an integer — and if yes, is this the correct result? Sure, there are intuitive answers to all these questions — but not when we’re trying to show the failings of intuition in the first place!
In the end, many students walk away with a suspicion that there’s something wrong with the proof, not that 0.9999… is really equal to 1.
Let’s try another one:
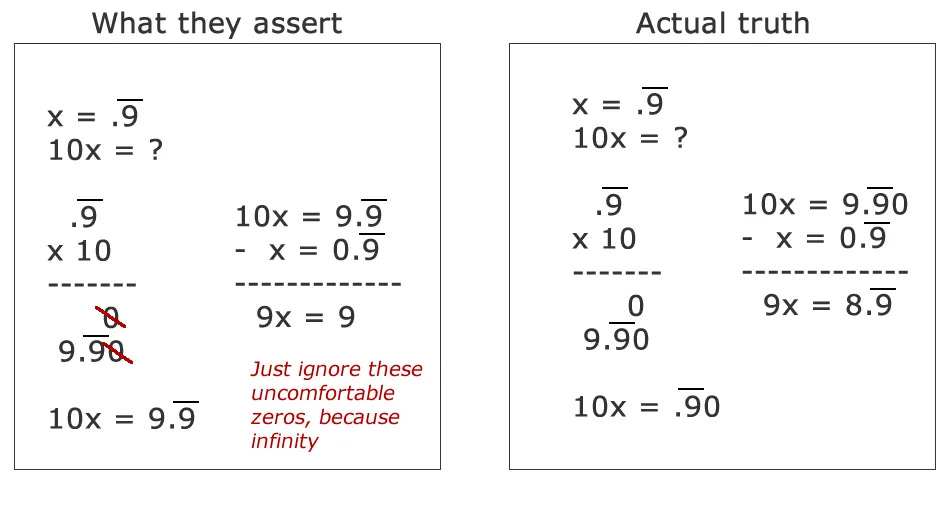
\(\begin{array}{c} x = 0.9999\ldots \\ \\ 10 \cdot x = 9.9999\ldots = 9 + \underbrace{0.9999\ldots}_{= \ x} = 9 + x \\ 9 \cdot x = 9 \implies x = 1 \end{array}\)
That’s even more suspect. We multiplied an infinite decimal expansion by 10. Did that add a zero at the “end”? A blogger exposes the shocking truth:
There are better proofs, but they usually resort to calculating limits of infinite sequences. Limits are unfamiliar to most and generally somewhat abstract; it doesn’t help that phrases such as "tends to” or “converges at infinity” sound nothing like the words we’re actually looking for: “equals” or “is”.
In the end, you have a bunch of websites strongly asserting that there’s absolutely no difference between 0.9999… and 1; and a network of “number skeptics” who claim that there must be some distance separating the values, no matter how small.
Oddly enough, there exists an intuitive way to reconcile these views. In his 2009 book, Ian Stewart starts with the following self-evident way to construct 0.999… to n decimal places:
\(0.9999... \textrm{ (to }n\textrm{ places)} = \frac{9}{10^1} + \frac{9}{10^2} + \ldots + \frac{9}{10^n}\)
We can rewrite any m-th element of the sum the following way:
\(\begin{align} \frac{9}{10^m} &= \frac{10-1}{10^m} = \\ \\ \frac{10}{10^{m}} - \frac{1}{10^m} &= \frac{1}{10^{m-1}} - \frac{1}{10^m} \end{align}\)
Applying this expansion, it becomes clear that all but the first and the last element of the expansion always cancel out; for example, for n = 3, we get:
\(\bigl(1 - \cancel{\frac{1}{10}} \bigr) + \bigl(\cancel{\frac{1}{10}} - \cancel{\frac{1}{100}} \bigr) + \bigl(\cancel{\frac{1}{100}} - \frac{1}{1000} \bigr) = 1 - \frac{1}{1000}\)
In other words, we arrive at the following form:
\(0.9999... \textrm{ (to }n\textrm{ places)} = 1 - {\bigl(\frac{1}{10}\bigr)}^n\)
At this point, it’s important to note that in the field of reals, there’s no notion of infinite or infinitesimal values. Reals can be arbitrarily big or small, but not infinitely big or small. The rule doesn’t have any cosmic significance; it’s just that to keep things simple, we define reals as an Archimedean group devoid of infinity-related singularities. The key tidbit is that if a and b are positive reals and a < b, there must exist some finite integer x that makes a · x > b. Infinite and infinitesimal quantities don’t obey that rule, so they’re not invited to the club.
The first practical consequence of this constraint is that when operating in the domain of real numbers, we can’t really declare that n = ∞ to calculate the infinite expansion of 0.9999…. That said, there is a fairly intuitive extension of reals, called hyperreals; they’re “backward-compatible” with reals but add infinite and infinitesimal numbers with some formal algebra for both.
In this system, (1/10)n nets an infinitesimal if n is infinite. That is to say, in the earlier formula, we end up with an infinitely small value that’s closer to 0 than any real can ever be:
\(0.9999... = 1 - \textrm{infinitesimal}\)
This result seems to undermine the claim that 0.9999… = 1, but let’s ponder what it means for one real number a to be different from another real number b. Fundamentally, it’s not about decimal expansions; by that standard, one could say that 0.5 ≠ 0.50. Instead, the essence of inequality between two reals can be stated this way: if you subtract a from b, the result must be a non-zero real number c.
This gets us to the crux of the matter: in our thought experiment, the difference between a and b is infinitesimal. This value can be represented in the domain of hyperreals, but it’s infinitely smaller than any non-zero real number we could possibly construct. Again, non-zero reals can be arbitrarily small, but not infinitely small: per the Archimedean property, they must “respond to” multiplication by an integer. The value of c doesn’t, so the only possible mapping of c onto reals is zero (to which it is infinitely close).
The beauty of this analysis is that it doesn’t reject intuition: you can continue to believe that there is something “missing” from 0.9999… that sets it apart from 1. It’s just that this something amounts to nothing in the particular algebra system we use day-to-day.







 English (US) ·
English (US) ·